Question

Write an explicit formula for the recursive formula shown below: A(n)=A(n-1)+3; A(1)=6

Answer 1

`a_n=A(n)=3n+3.`

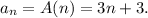
Explanation:

You are given recursive formula
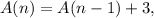`A(n)=A(n-1)+3,` where
`A(1)=6.`

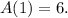
Find some terms of the sequence:

`a_1=A(1)=6,\\ \\a_2=A(2)=A(1)+3=6+3=9,\\ \\a_3=A(3)=A(2)+3=9+3=12,\\ \\a_4=A(4)=A(3)+3=12+3=15,...`

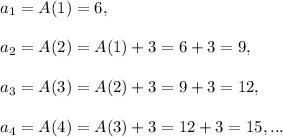
You van see that these terms form the arithmetic sequence with first term
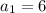`a_1=6` and difference
`d=3.`

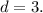
An explicit formula for n-th term of arithmetic sequence is

`a_n=a_1+(n-1)d.`

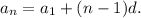
In your case,

`a_n=6+(n-1)\cdot 3,\\ \\a_n=6+3n-3,\\ \\a_n=3n+3.`