Question

Two events E1 and E2 are called independent if p(E1 â© E2) = p(E1)p(E2). For each of the following pairs of events, which are subsets of the set of all possible outcomes when a coin is tossed three times, determine whether or not they are independent. a) E1: tails comes up with the coin is tossed the first time; E2: heads comes up when the coin is tossed the second time. b) E1: the first coin comes up tails; E2: two, and not three, heads come up in a row. c) E1: the second coin comes up tails; E2: two, and not three, heads come up in a row.

Answer 1

P (E1) = 18 / 38

P (E2) = 18 / 38

P (E1 and E2) = 10 / 38

Explanation:

Answer 2

Answer: a) Independent

b) Independent

c) Dependent

Explanation:

Since, If a coin is tossed three times,

Then, total number of outcomes, n(S) = 8

a)
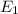`E_1` : tails comes up with the coin is tossed the first time;

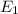`E_1` = { TTT, THH, THT, TTH }

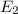`E_2` : heads comes up when the coin is tossed the second time.

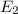`E_2` = { THT, HHH, THH, HHT }

Thus,
`n(E_1)=4`

⇒
`P(E_1)=(n(E_1))/(n(S))=(4)/(8)=(1)/(2)`

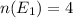
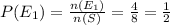
Similarly,
`P(E_2)=(1)/(2)`

⇒
`P(E_1)* P(E_2)=(1)/(2)* (1)/(2)=(1)/(4)`

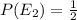
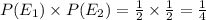
Since,
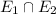`E_1\cap E_2` = { THH, THT }

`n(E_1\cap E_2) = 2`

⇒
`P(E_1\cap E_2) = (n(E_1\cap E_2))/(n(S))= (2)/(8)=(1)/(4)`

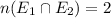
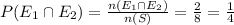
Thus,
`P(E_1\cap E_2)=P(E_1)*P(E_2)`

Therefore,
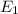`E_1` and
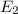`E_2` are independent events.

B)
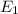`E_1` : the first coin comes up tails

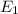`E_1` = { TTT, THH, THT, TTH }

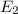`E_2` : two, and not three, heads come up in a row

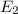`E_2` = { HHT, THH }

Thus,
`n(E_1)=4`

⇒
`P(E_1)=(n(E_1))/(n(S))=(4)/(8)=(1)/(2)`

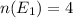
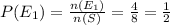
Similarly,
`P(E_2)=(1)/(4)`

⇒
`P(E_1)* P(E_2)=(1)/(2)* (1)/(4)=(1)/(8)`

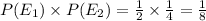
Since,
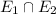`E_1\cap E_2` = { THH }

`n(E_1\cap E_2) = 1`

⇒
`P(E_1\cap E_2) = (n(E_1\cap E_2))/(n(S))= (1)/(8)`

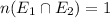
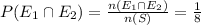
Thus,
`P(E_1\cap E_2)=P(E_1)*P(E_2)`

Therefore,
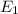`E_1` and
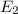`E_2` are independent events.

C)
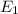`E_1` : the second coin comes up tails;

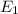`E_1` = { HTH, HTT, TTT, TTH }

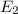`E_2` : two, and not three, heads come up in a row

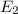`E_2` = { HHT, THH }

Thus,
`n(E_1)=4`

⇒
`P(E_1)=(n(E_1))/(n(S))=(4)/(8)=(1)/(2)`

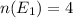
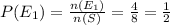
Similarly,
`P(E_2)=(1)/(4)`

⇒
`P(E_1)* P(E_2)=(1)/(2)* (1)/(4)=(1)/(8)`

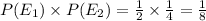
Since,
`E_1\cap E_2` =
`\phi`

`n(E_1\cap E_2) = 0`

⇒
`P(E_1\cap E_2) = 0`

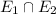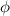
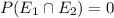
Thus,
`P(E_1\cap E_2)\\eq P(E_1)*P(E_2)`

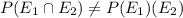
Therefore,
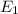`E_1` and
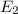`E_2` are dependent events.