Question

In △ABC, CM is the median to AB and side BC is 12 cm long. There is a point P∈ CM and a line AP intersecting BC at point Q. Find the lengths of segments CQ and BQ , if P is the midpoint of CM

Answer 1

CQ=4 cm, BQ=8 cm

Explanation:

In given triangle ABC draw the line MD parallel to the AQ.

1. Consider triangle AMD. In this triangle PQ║MD (build) and CP=PM (P is midpoint of CM). Then by the triangle midline theorem, line PQ is midline of triangle AMD and CQ=QD.

2. Consider triangle BAQ. In this triangle AQ║MD and AM=MB. Then by the triangle midline theorem, line MD is midline of triangle BAQ and BD=QD.

Hence, CQ=QD=BD. Since BC=12 cm and

BC=BQ+QD+BD,

then

`CQ=QD=BD=(12)/(3)=4\ cm.`

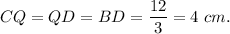
Note that

BQ=BD+QD=4+4=8 cm.