Question

50 points. Can anyone give an example of a noncommutative ring that doesn't involve matrices?

Answer 1

Hamilton's quaternions are an example of non-commutative ring. If you are not familiar with them, they are similar to complex numbers, except for the fact that there are three roots of -1: the ring is generated by

`H = <1, i, j, k>`

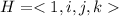
Which means that a generic element is appears as follows:

`z = a+bi+cj+dk,\quad a,b,c,d \in \mathbb{R}`

The rules for additions are the usual: you sum like terms. As for the mutliplicaitons, you work like this:

`ij = k,\quad kj = i,\quad ki = j,\quad ji = -k,\quad kj = -i,\quad ik = -j`