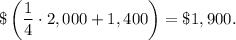Answer:
The first year Sam invested $2,000. The third year sally invested $1,900.
Explanation:
Let $x be the amount of money Sam invested the first year. The second year, he invested $2,000 less than 5/2 times the amount he invested the first year, then the second year he invested
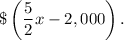
The third year, he invested $1,000 more than 1/5 of the amount he invested the first year, then the third year he invested
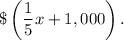
During three years Sam invested
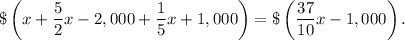
The first year, Sally invested $1,000 less than 3/2 times the amount Sam invested the first year, then the first year she invested
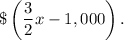
The second year, she invested $1,500 less than 2 times the amount Sam invested the first year, then the second year she invested
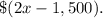
The third year, she invested $1,400 more than 1/4 of the amount Sam invested the first year, then the third year she invested
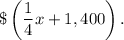
During three years Sally invested
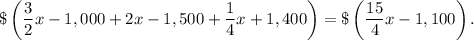
If Sam and Sally invested the same total amount at the end of three years, then
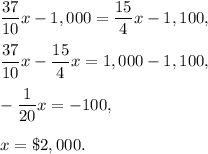
Thus,