Answer:
Explanation:
Ok so first of all, we have to find what point on the x axis make the distance between the other two equidistant. So the distance from (2,-5) to (x,0) has to be the same distance from (x,0) to (-2,9). This becomes
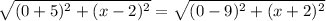
Squaring both sides and simplifying we get

The x^2's and 4's cancel out. Then subtract 81 and 4x from both sides

Then solving
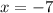
So we know the point is (-7,0)
So finding the distance is plugging -7 into either one of those. So it becomes
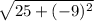
This is plugging -7 into
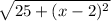
Calculating we get
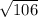
So we have an isosceles triangle with both sides sqrt of 106. To find the are of a triangle we need the base and height. The height and base are going to be challenging. To find the height, we first need to find the slope of the first two points. Using (y₂-y₁)/(x₂-x₁)the slope is -7/2. The line perpendicular to that (the height) is
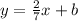
The slope is opposite and reciprocal so its 2/7. Plugging in (-7,0) because it's a solution to the line. So it becomes
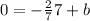
Solving you get b = 2 so the equation of the line for the height is
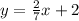
For the line for the base it is
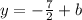
Plugging any one of the two points and solving would get us
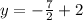
To find the height we need the point of intersection. To do this we set the equations equal to each other. If you notice the b's are both +2 so that is the intersection. (0,2)
So finding the distance from (-7,0) to (0,2) is the sqrt of 53. Now to find the base. This is just the distance from (-2,9) and (2,-5). Using the distance formula or building a right triangle you will get 2sqrt(53). Now just use the formula of a triangle which is bh/2, we get (2√(53)×√53)/2. The two's cancel out and the sqrt's go away, and so the are of the triangle is 53.