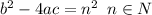Question

Compare using the quadratic formula to find solutions to a quadratic equation having irrational roots to that of one that has rational roots.

Answer 1

For a general quadratic equation with rational coefficients

`ax^2+bx+c=0,\,\,\,\,a,b,c \in Q`

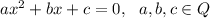
the two solutions are:

`x_(1,2) = (-b\pm√(b^2-4ac))/(2a)=(-b\pm√(D))/(2a)`

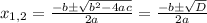
where D is the determinant.

Clearly, a solution will a rational number as long as
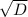`√(D)` is rational. However, it can be shown that a square root of an integer is only rational if its value is an integer. In other words,
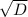`√(D)` is rational if and only if the determinant is a perfect square,
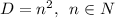`D=n^2, \,\,\,n\in N`, otherwise the square root is irrational. Therefore the coefficients of quadratic equations that are to have rational solutions must satisfy the following condition:

`b^2-4ac=n^2\,\,\,n\in N`