Question

Differentiate t²sin(2t)​

Answer 1

`\displaystyle \large{y\prime = 2t \sin (2t) + 2t^2 \cos (2t)}`

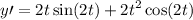
Explanation:

We are given a function:

`\displaystyle \large{y = t^2 \sin (2t)}`

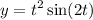
To differentiate a function, we are going to use the product rules since there are two functions which are t^2 and sin(2t) multiplying together.

From the product rules,
`\displaystyle \large{y = f(x)g(x) \to y\prime = f\prime (x) g(x)+f(x) g\prime (x)}`

Therefore,
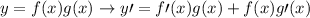
`\displaystyle \large{y = t^2 \sin (2t) \to y\prime = (t^2)\prime \sin (2t) + t^2 (\sin (2t))\prime}`

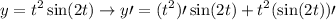
Before we start differentiating, I’d like you to look at [sin(2t)]’. A function like this, you cannot just directly derive and answer. You need to use chain rules.

We know that,
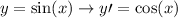`\displaystyle \large{y = \sin (x) \to y\prime = \cos (x)}` but what if the “x” is another function? Like sin(3x), sin(x^2) as examples. The insides are another function, can be expressed as fog(x) or gof(x) is composite function.

Basically, chain rule is a rule or formula for composite function and it’s the most common and useful as well as being always used in differentiation.

Chain Rules

`\displaystyle \large{(dy)/(dx) = (dy)/(du) (du)/(dx)}`

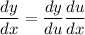
where u is another function in a bracket. From the formula above, it can be also written as:

`\displaystyle \large{[f(g(x))]\prime = f(g(x))\prime \cdot g(x)\prime`

To simply say, you differentiate the whole function first then multiply with the chain or inner derived function.

So from the function, we obtain:

`\displaystyle \large{y\prime = 2t \sin (2t) + t^2 \cos (2t) \cdot (2t)\prime}\\ \displaystyle \large{y\prime = 2t \sin (2t) + t^2 \cos (2t) \cdot 2}\\ \displaystyle \large{y\prime = 2t \sin (2t) + 2t^2 \cos (2t)}`

The factored form would be:

`\displaystyle \large{y\prime = 2t ( \sin (2t) + t \cos (2t))}`

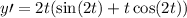
From above, for polynomial function, to differentiate, you can do by using the power rules.

Power Rules

`\displaystyle \large{y = ax^n \to y\prime = nax^(n-1)}`