Answer:
y = (x + 9)² - 4
Explanation:
Hello!
The current form of the equation is in Standard Form:
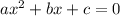
We want to convert it into Vertex Form:
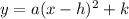
We can do this by Completing The Square.
What is Completing The Square?
Completing the square is when you solve a quadratic by having a Perfect Square on one side. Essentially you want to factor a perfect Square Trinomial by adding your own value to both sides so it makes it possible. You can only complete the square when the coefficient of the x-variable is 1.
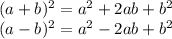
To create a perfect square from Standard Form (ax² + bx + c = 0):
- Take the b-value
- Divide it by 2
- Square it
- Add it to both Sides
Now, let's try it with our equation.
Complete the Square
Replace y with 0
Complete the Square
Use the 81 to convert it into a Perfect Square. (
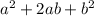 )
)
Subtract 81 from both sides
Therefore, the equation in Vertex Form is
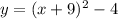 .
.
Difference between Perfect Square Factoring and Regular Factoring
Factoring this equation regularly will give us (x + 7)(x + 11) = y.
But we want both factors to be the same, so that it is the square of one factor.
Since there is another term being added that will not give us a perfect square, we have to add a completely new term to factor it into a Perfect Square (81), and factor using that term rather than 77. This is how we got it:
y = (x + 9)² - 4
Expanding (x + 9)² will give us x² + 18x + 81, not the same as x² + 18x + 77. That's why we subtracted 4 at the end.
Another simple way to Complete the Square:
Ignore the term with no variable completely (77) and focus on x² + 18x.
If you want to factor it into a perfect square, we have to add something to it.
Using the Formula
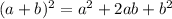 , we know that "A" is 1, as the coefficient of x is 1. "2" times "1" times "b" is 18, so b would be 9.
, we know that "A" is 1, as the coefficient of x is 1. "2" times "1" times "b" is 18, so b would be 9.
Add the square of 9 to both sides to get 81. Then, factor it using the formula.
- y + 81 = x² + 18x + 81
- y + 81 = (x + 9)²
Subtract the 81 from the left-hand side, and finally, add the 77 that we left out at the start.
It's pretty much the same concept as the first method, but once we organize it a bit better, it works faster and is not as chaotic.
There is also a third way: Finding the Vertex
Vertex Form is named what it is for a reason.
It's because the Vertex is inside the Equation. In
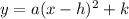 the vertex is (h,k).
the vertex is (h,k).
We can find the x-value of the vertex from the Standard Form: ax² + bx + c
Plug in the value of -9 into the equation to find the y-value of the vertex
So the vertex would be (-9,-4).
Plugging that into the formula, we get
 . A is 1 since the coefficient of x is 1.
. A is 1 since the coefficient of x is 1.