Question

What is the approximate value of y - x

Answer 1

17.2°

Explanation:

using the tangent ration in the right triangle

tan y° =
`(opposite)/(adjacent)` =
`(19.1)/(14.1)`, hence

y =
`tan^(-1)`(
`(19.1)/(14.1)`) ≈ 53.6°

tan x° =
`(14.1)/(19.1)`, hence

x =
`tan^(-1)`(
`(14.1)/(19.1)`) ≈ 36.4°

y - x = 53.6° - 36.4° = 17.2°

Answer 2

D) y -x = Approximate 17.1 degree.

Explanation:

Given : Triangle .

To find : Approximate value of y - x.

Solution : We have given a right angle triangle with

Opposite side = 19.1 in.

Adjacent side = 14 .1 in.

Tan( y ) =
`(Opposite)/(adjacent)`.

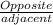Plug the values

Tan( y ) =
`(19.1)/(14.1)`.

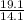tan(y) = 1.354.

Taking tan inverse both sides.

y =
`tan^(-1)(1.354)`.

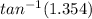y = 53.55 degree.

Now, by the sum of angle of triangles is 180 degree.

Angle c + angle y + angle x = 180.

Plug the variable

90 + 53.55 + x = 180.

83.55 + x = 180

On subtracting both sides by 83.55

x = 36.45 degree

Then ,

y - x = 53 .55 - 36 . 45

y - x = 17.2

Approximate 17.1 degree

Therefore, D) y -x = Approximate 17.1 degree.