Answer:
Exactly 12 years it will take for these trees to be the same height
Explanation:
Slope intercept form: An equation of line is in the form of
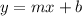 where m is the slope or unit rate and b is the y-intercepts.
where m is the slope or unit rate and b is the y-intercepts.
Let x represents the time in years and y represents the height of the tree.
Use conversion:
1 ft = 12 inches
As per the given statement:
Type A is 8 feet tall and grows at a rate of 3 inches per year.
⇒unit rate per year = 3 inches =
 ft
ft
Then, we have;
 ......[1]
......[1]
Similarly for;
Type B is 7 feet tall and grows at a rate of 4 inches per year.
⇒unit rate per year = 4 inches =
 ft
ft
then;
 .....[2]
.....[2]
To find after how many years it will take for these trees to be the same height.
Since, trees to be the same height;
⇒equate [1] and [2], to solve for x;
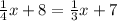
Subtract 7 from both sides we get;
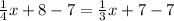
Simplify:
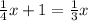
Subtract
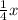 from both sides we get;
from both sides we get;
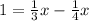
Simplify:
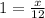
Multiply both sides by 12 we get;
x = 12
Therefore, exactly it will take for these trees to be the same height is, 12 years