Question

At a horse show, ribbons are awarded for first, second, third, and fourth places. There are 16 horses in the show. How many different arrangements of four horses are possible?

Answer 1

43680 different arrangements are possible.

Explanation:

The total number of horses are :16

We have to find different arrangement of four horses

Since, we have to find arrangements means we will use permutation

So, the required arrangement will be:

`^(16)P_4`

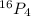
Now, using:
`^(n)P_r=(n!)/((n-r)!)`

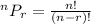
Here, n= 16 and r=4 on substituting the values we get:

`^(16)P_4=(16!)/((16-4)!)`

`\Rightarrow (16!)/(12!)`

`\Rightarrow (16\cdot 15\cdot 14\cdot 13\cdot 12!)/(12!)`

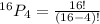
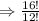
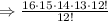
Cancel out the common term that is 12! we get:

`16\cdot 15\cdot 14\cdot 13`

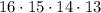
After simplification we get: 43680

Hence, 43680 different arrangements are possible.