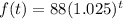Question

The population of a pack of wolves is 88. The population is expected to grow at a rate of 2.5% each year.

Which function equation represents the population of the pack of wolves after t years?

f(t)=88(0.025)^t

f(t)=88(1.025)^t

f(t)=88(1.25)^t

f(t)=88(2.5)^t

Answer 1

Option B is correct.

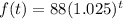`f(t) = 88(1.025)^t` represents the population of the pack of wolves after t years

Explanation:

The exponential growth function is given by;

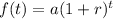`f(t) = a(1+r)^t` ......[1]

where

a represented the initial value

r represents the rate(in decimal)

t represents the time in years

As per the given statement: The population of a pack of wolves is 88. Also, the population is expected to grow at a rate of 2.5% each year.

⇒ a = 88 and r =2.5% = 0.025.

Substituting these values in equation [1], we have;

`f(t) = 88(1+0.025)^t`

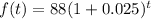
or

`f(t) = 88(1.025)^t`

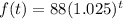
Therefore, the population model of the pack of wolves after t years is given by:
`f(t) = 88(1.025)^t`