Answer:
4, 2, 1,
 ,
,
 , .....
, .....
Explanation:
Fifth term (a₅) =

Common ratio (r) =

n = 5
The formula to find the
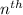 term of a geometric sequence is
term of a geometric sequence is
a₅ = a₁r⁽ⁿ⁻¹⁾
=>
 = a₁*
= a₁*
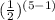
=>
 = a₁*
= a₁*
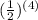
=>
 = a₁*
= a₁*

=>
 = a₁*
= a₁*
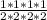
=>
 = a₁*
= a₁*
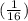
Flip the sides of the equation
a₁*
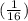 =
=

Multiply both sides by 16
a₁*
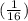 *16 =
*16 =
 *16
*16
Cancelling out the 16's from the top and bottom of the left side
a₁ =
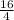
=> a₁ = 4
So, first term of the geometric sequence is 4.
Common ratio =

Second term = First term * Common ratio
= 4*

=
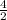
= 2
Third term = Second Term * Common ratio
= 2 *

=
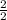
= 1
Fourth term = Third Term * Common ratio
= 1 *

=

Fifth term (given) =

So, the geometric sequence would be
4, 2, 1,
 ,
,
 , .....
, .....