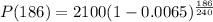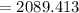Question

a quantity with an initial value of 2100 decades exponentially at a rate of 0.65% every 10 days what is the value of the quantity after 186 hours to the nearest hundredth

Answer 1

Q(186) = 2089.463

Explanation:

Formula for decaying exponentially:

Q(t) = Q_0 e^{-rt}

where, Q(t)= quantity at time t

Q_0 = initial quantity value (2100)

t = time (186 hours)

r = rate of decaying (0.65)

r = 0.65% = 10 days

1 day =
`(0.0065)/(10)`

1 hour =
`(0.0065)/(240)`

186 hours =
`(0.0065*186)/(240)`

rt = 0.00503

Q(186) = 2100*e^{-0.00503}

= 2089.46

Answer 2

The value of the quantity after 186 hours is 2089.41

Explanation:

We can use exponential formula

`P(t)=a(1-b)^{(t)/(h) }`

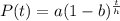
a quantity with an initial value of 2100

so,

`a=2100`

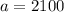
decays exponentially at a rate of 0.65% every 10 days

So, b=0.0065 when h=10*24=240

now, we can plug values

`P(t)=2100(1-0.0065)^{(t)/(240) }`

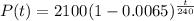
now, we can plug t=186

and we get

`P(186)=2100(1-0.0065)^{(186)/(240) }`

`=2089.413`