Steps:
- Discriminant Formula: D = b² - 4ac (With a = x² coefficient, b = x coefficient, and c = constant)
So to find the number of solutions this quadratic equation has without actually solving the equation, we are going to be using the discriminant formula. Plug in the numbers and solve:
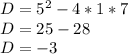
Now, here are the rules with discriminants:
- D > 0; there are 2 real solutions in the equation
- D = 0; there is 1 real solution in the equation
- D < 0; there are no real solutions in the equation
Answer:
Since -3 is less than 0, this means that there are 0 real solutions in this equation.