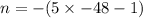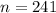Question

HELP ASAP : Find the largest value of n such that 5x^2+nx+48 can be factored as the product of two linear factors with integer coefficients

Answer 1

`n=241`

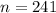
Explanation:

We are given

`5x^2+nx+48`

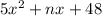
Let's assume it can be factored as

`5x^2+nx+48=(5x-s)(x-r)`

now, we can multiply right side

and then we can compare it

`5x^2+nx+48=5x^2-5rx-sx+rs`

`5x^2+nx+48=5x^2-(5r+s)x+rs`

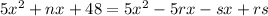
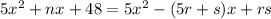
now, we can compare coefficients

`rs=48`

`5r+s=-n`

`n=-(5r+s)`

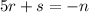
now, we can find all possible factors of 48

and then we can assume possible prime factors of 48

`48=-+(1* 48)`

`48=-+(2* 24)`

`48=-+(3* 16)`

`48=-+(4* 12)`

`48=-+(6* 8)`

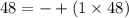
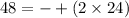
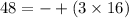
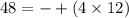
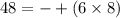
Since, we have to find the largest value of n

So, we will get consider larger value of r because of 5r

and because n is negative of 5r+s

so, we will both n and r as negative

So, we can assume

r=-48 and s=-1

so, we get

`n=-(5* -48-1)`

`n=241`