Question

AB is dilated by a scale factor of 3 to form AB . Point O is the center of dilation, and point O lies on AB . If the slope of AB is 3, what can be said about line A'B' ?

A. The slope of is 6, but does not pass through O.

B. The slope of is 9, and passes through O.

C. The slope of is 9, but does not pass through O.

D. The slope of is 3, and passes through O.

E. The slope of is 3, but does not pass through O.

Answer 1

Explanation:

Answer 2

Option: D is the correct answer.

D. The slope of is 3, and passes through O.

Explanation:

It is given that:

AB is dilated by a scale factor of 3 to form AB .

Also, the line AB pass through the origin.

So, if AB pass through (0,0) and some point (x,y) then the slope of line AB is:

`Slope=(y-0)/(x-0)\\\\i.e.\\\\Slope=(y)/(x)=3`

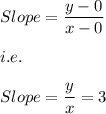
( Since, it is given the slope of AB is 3 )

Now , if AB is dilated to A'B' by a scale factor of 3 then

(0,0) → (0,0)

and

(x,y) → (3x,3y)

i.e. (0,0) and (3x,3y) will lie on A'B'.

Hence, the slope of line A'B' is given by:

`Slope=(3y-0)/(3x-0)\\\\i.e.\\\\Slope=(3y)/(3x)\\\\i.e.\\\\Slope=(y)/(x)=3`

Hence, both have the same slope.

The answer is : Option: D