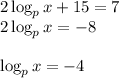Answer:
For #3:
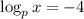
Explanation:
I'm a little rusty on my logarithm rules for #2, but here's an explanation of #3.
Logarithms: the Inverse of Exponents
In a sense, we can think of operations like subtraction and division as different ways of representing addition and multiplication. For instance, the same relationship described by the equation 2 + 3 = 5 is captured in the equation 5 - 3 = 2, and 5 × 2 = 10 can be restated as 10 ÷ 2 = 5 without any loss of meaning.
Logarithms do the same thing for exponents: the expression
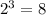 can be expressed in logarithms as
can be expressed in logarithms as
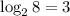 . Put another way, logarithms are a sort of way of pulling an exponent out onto its own side of the equals sign.
. Put another way, logarithms are a sort of way of pulling an exponent out onto its own side of the equals sign.
The Problem
Our problem gives us two facts to start: that
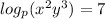 and
and
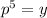 . With that, we're expected to find the value of
. With that, we're expected to find the value of
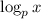 .
.
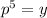 stands out as the odd-equation-out here; it's the only one not in terms of logarithms. We can fix that by rewriting it as the equivalent statement
stands out as the odd-equation-out here; it's the only one not in terms of logarithms. We can fix that by rewriting it as the equivalent statement
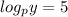 . Now, let's unpack that first logarithm.
. Now, let's unpack that first logarithm.
Justifying Some Logarithm Rules
For a refresher, let's talk about some of the rules logarithms follow and why they follow them:
Product Rule:
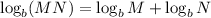
The product rule turns multiplication in the argument (parentheses) of a logarithm into addition. For a proof of this, consider two numbers
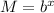 and
and
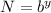 . We could rewrite these two equations with logarithms as
. We could rewrite these two equations with logarithms as
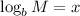 and
and
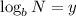 . With those in mind, we could say the following:
. With those in mind, we could say the following:
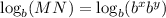 (Substitution)
(Substitution)
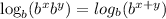 (Laws of exponents)
(Laws of exponents)
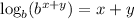 (
(
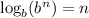 )
)
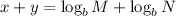 (Substitution)
(Substitution)
And we have our proof.
Exponent Rule:
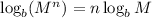
Since exponents can be thought of as abbreviations for repeated multiplication, we can rewrite
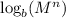 as
as
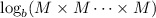 , where M is being multiplied by itself n times. From there, we can use the product rule to rewrite our logarithm as the sum
, where M is being multiplied by itself n times. From there, we can use the product rule to rewrite our logarithm as the sum
 , and since we have the term
, and since we have the term
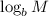 added n times, we can rewrite is as
added n times, we can rewrite is as
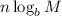 , proving the rule.
, proving the rule.
Solving the Problem
With those rules in hand, we're ready to solve the problem. Looking at the equation
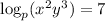 , we can use the product rule to split the logarithm into the sum
, we can use the product rule to split the logarithm into the sum
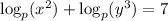 , and then use the product rule to turn the exponents in each logarithm's argument into coefficients, giving the equation
, and then use the product rule to turn the exponents in each logarithm's argument into coefficients, giving the equation
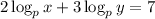 .
.
Remember how earlier we rewrote
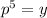 as
as
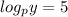 ? We can now use that fact to substitute 5 in for
? We can now use that fact to substitute 5 in for
 , giving us
, giving us

From here, we can simply solve the equation for
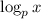 :
: