Question

Diagonal AC divides the trapezoid ABCD (with bases AD and BC , AD>BC) into two similar triangles, △ABC and △DCA. Find AC if BC=4 cm and AD=9 cm.

Answer 1

AC= 6 cm

Explanation:

It is given that ABCD is a trapezoid

Also AC divides the trapezoid into two similar triangles

ΔABC≈ΔDCA

The ratio of corresponding sides of similar triangles are equal, so we have

`(AB)/(CD) =(BC)/(AC) =(AC)/(AD)`

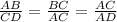
now we can take

`(BC)/(AC) =(AC)/(AD)`

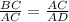
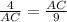`(4)/(AC) =(AC)/(9)` ( since BC=4 and AD= 9)

now we cross multiply

`4(9)=AC^(2)`

`AC^(2)=36`

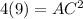
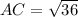`AC=√(36)` (taking square root )

AC= 6 cm