Question

Peter calculated that the theoretical probability of obtaining exactly two heads when flipping six coins is 23.4%. What number of heads also has a 23.4% theoretical probability of coming up when 6 coins are flipped?

Answer 1

The theoretical probability of obtaining exactly four heads when flipping six coins is also 23.4%.

Explanation:

Getting x successes out of n trials is a binomial distribution and is given by:

p(x) =
`nC_(x) p^(n-x) q^(x)`

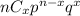
Here, n = 6

x = 2

p = probability of one head =
`(1)/(2)`

q = 1 - p

=
`1-(1)/(2)`

=
`(1)/(2)`

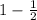
Substitute these values, we get,

p(2) =
`6C_(2) ((1)/(2) )^(6-2) ((1)/(2) )^(2)`

=
`15((1)/(2) )^(6)`

=
`(15)/(64)`

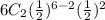
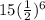
= 0.234

= 23.4%

We know that
`6C_(2) =6C_(6-2)`

`6C_(2) =6C_(4)`

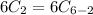
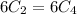
Now,

p(4) =
`6C_(4) ((1)/(2) )^(6-4) ((1)/(2) )^(4)`

=
`15((1)/(2) )^(6)`

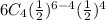
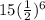
= p(2)

Hence, the theoretical probability of obtaining exactly four heads when flipping six coins is also 23.4%.