Question

Find the area of the shaded region.

Answer 1

We know that : If in a Circle of Radius 'r', an Arc of length 'l' subtends an Angle 'θ' radian at the Centre then Relation between them is given by :

✿
`\mathsf{\theta = (l)/(r)}`

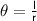
Given : The Arc Length of the Larger Sector = 12 m

Given : θ = 1 radian

`\mathsf{\implies 1 = (12)/(Radius\;of\;the\;Larger\;Sector)}`

`\mathsf{\implies Radius\;of\;the\;Larger\;Sector = 12m}`

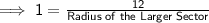
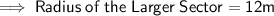
Given : The Arc Length of the Smaller Sector = 8 m

`\mathsf{\implies 1 = (8)/(Radius\;of\;the\;Smaller\;Sector)}`

`\mathsf{\implies Radius\;of\;the\;Smaller\;Sector = 8m}`

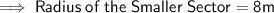
The Way to look at this Solution is to Realize that : If we Subtract the Area of Smaller Sector from the Area of Larger Sector, we will end up with the Area of the Shaded Region.

We know that : Area of a Sector with Radius r is given by :
`\mathsf{(1)/(2)(r)^2\theta}`

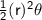
where : θ is the Angle subtended (in Radians)

`\mathsf{\implies Area\;of\;the\;Larger\;Sector = (1)/(2)(12)^2(1)}`

`\mathsf{\implies Area\;of\;the\;Larger\;Sector = (144)/(2)}`

`\mathsf{\implies Area\;of\;the\;Larger\;Sector = 72m^2}`

`\mathsf{\implies Area\;of\;the\;Smaller\;Sector = (1)/(2)(8)^2(1)}`

`\mathsf{\implies Area\;of\;the\;Smaller\;Sector = (64)/(2)}`

`\mathsf{\implies Area\;of\;the\;Smaller\;Sector = 32m^2}`

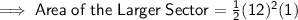
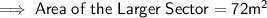
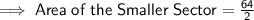
Area of the Shaded Region = (72 - 32) = 40m²