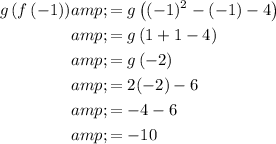Question

Pls help to solve these 4 questions MAX POINTS

Answer 1

`\textsf{23.} \quad \left((f)/(g)\right)(x) = (x^2-x-4)/(2x-6)`

`\textsf{24.} \quad \left(f \circ g\right)(x) =4x^2-26x+38`

`\textsf{25.} \quad \left(g \circ f \right)(x) =2x^2-2x-14`

`\textsf{26.} \quad g\left(f\left(-1\right)\right)=-10`

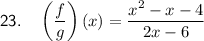
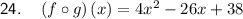
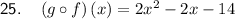
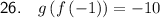
Explanation:

Given functions:

`\begin{cases}f(x)=x^2-x-4\\g(x)=2x-6\end{cases}`

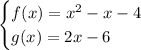
Function composition is an operation that takes two functions and produces a third function.

Question 23

The composite function (f/g)(x) means to divide function f(x) by function g(x):

`\begin{aligned}\left((f)/(g)\right)(x) & = (f(x))/(g(x))\\& = (x^2-x-4)/(2x-6)\end{aligned}`

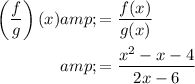
Question 24

The composite function (f o g)(x) means to substitute function g(x) in place of the x in function f(x):

`\begin{aligned}\left(f \circ g\right)(x) & = f\left[g(x)\right]\\& = f(2x-6)\\& =(2x-6)^2-(2x-6)-4\\& =(2x-6)(2x-6)-2x+6-4\\& =4x^2-24x+36-2x+2\\& =4x^2-24x-2x+36+2\\& =4x^2-26x+38\end{aligned}`

Question 25

The composite function (g o f)(x) means to substitute function f(x) in place of the x in function g(x):

`\begin{aligned}\left(g \circ f \right)(x) & = g\left[f(x)\right]\\& = g(x^2-x-4)\\&=2(x^2-x-4)-6\\&=2x^2-2x-8-6\\&=2x^2-2x-14\end{aligned}`

Question 26

The composite function g(f(-1)) means to substitute x = -1 into function f(x) then substitute this result in place of the x in function g(x):

`\begin{aligned}g\left(f\left(-1\right)\right) & = g\left((-1)^2-(-1)-4\right)\\& = g\left(1+1-4\right)\\& = g\left(-2\right)\\&=2(-2)-6\\&=-4-6\\&=-10\end{aligned}`