Question

Suppose △ABC and △DEF are similar and BC=6, EF=8, DF-AC=1. Find DF.

Answer 1

Side DF = 4 units

Explanation:

Similar triangles states that the triangles with equal corresponding angles and proportionate sides.

Given: ΔABC and ΔDEF are similar

Corresponding angles are;

`\angle A = \angle D` ,

`\angle B = \angle C` ,

`\angle C= \angle F`

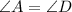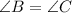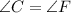
Proportionate sides are;

`(AB)/(DE) =(BC)/(EF) =(AC)/(DF)`

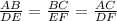
It is also given BC = 6 units , EF = 8 units and DF -AC = 1

Let AC = x units then;

DF = x +1 units.

Then, by definition of similar triangle ;

`(BC)/(EF) =(AC)/(DF)`

`(6)/(8) =(x)/(x+1)`

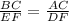
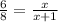
By cross multiply we have;

`6(x+1) = 8x`

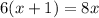
Using distributive property;
`a\cdot(b+c) = a\cdot b+ a\cdot c`

6x + 6 = 8x

Subtract 6x on both sides we get;

6x + 6 -6x = 8x -6x

Simplify:

6 = 2x

Divide by 2 on both sides we get;

x = 3

DF = x +1 = 3+1 = 4

Therefore, the side DF is, 4 units