Question

Triangles △ABC and △DEF are similar. Find the lengths of the sides of △DEF, if AB=2 cm, BC=3 cm, CA=4 cm, DE=1.5 cm.

Answer 1

DF=3.0cm, EF=3cm

Explanation:

Given: ΔABC is similar to ΔDEF,

Therefore:
`(AB)/(DE) =(AC)/(DF)`

⇒
`(2)/(1.5)= (4)/(DF)`

⇒ DF=3.0cm

Now, by the similarity of triangles, we have Ef=3cm.

Answer 2

The sides of △DEF are DE = 1.5cm, DF = 3cm, and EF= 2.25 cm.

Explanation:

We know that

`\triangle ABC \sim \triangle DE\ F`

`AB=2cm\\BC=3cm\\CA=4cm\\DE=1.5cm`

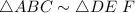
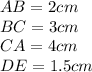
Remember that a similarity between two triangles represent a proportional relation between corresponding side. In this case, such proportions are

`(AB)/(DE)=(BC)/(EF)=(AC)/(DF)`

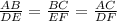
So, we have to find sides DF and EF. Using given values, we have

`(AB)/(DE)=(BC)/(EF)\\ (2)/(1.5)=(3)/(EF)\\ EF=(3(1.5))/(2)=2.25`

Then,

`(AB)/(DE)=(AC)/(DF)\\(2)/(1.5)=(4)/(DF)\\ \\DF=(4(1.5))/(2)=3`

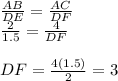
Therefore, the sides of △DEF are DE = 1.5cm, DF = 3cm, and EF= 2.25 cm.