Question

What is x and y if you have 4x-2y=5 and y=2x+10

Answer 1

`\bf \begin{cases} 4x-2y=5\\ \boxed{y}=2x+10 \end{cases}~\hspace{7em}\stackrel{\textit{substituting \boxed{y} in the 1st equation}}{4x-2\left( \boxed{2x+10} \right)=5} \\\\\\ 4x-4x-20=5\implies -20\\e 5`

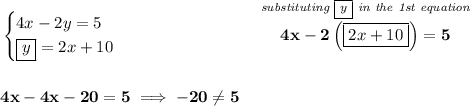
which makes no sense, our variable went poof, but that is a flag that this system has no solution, let's quickly solve both for "y" to put them in slope-intercept form,

`\bf 4x-2y=5\implies 4x-5=2y\implies \cfrac{4x-5}{2}=y\implies ~\hfill \stackrel{\stackrel{m}{\downarrow }}{2}x-\cfrac{5}{2}=y \\\\\\ ~\hfill y=\stackrel{\stackrel{m}{\downarrow }}{2}x+10`

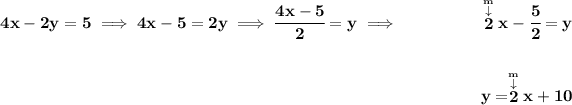
so, notice, the slopes(m) are exactly the same for both, whilst the y-intercept differs, meaning both lines are parallel and therefore never touch each other, thus, no solution.

the untrue equation of -20 = 5, is another way to say, "no solution".