Answer:
( -1,-5 )
Explanation:
We have the co-ordinates A( -3,3 ), B( -1,7 ) and C( 3,3 ).
We will find the orthocenter using below steps:
1. First, we find the equations of AB and BC.
The general form of a line is y=mx+b where m is the slope and b is the y-intercept.
Using the formula of slope given by
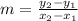 , we will find the slope of AB and BC.
, we will find the slope of AB and BC.
Now, slope of AB is
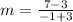 i.e.
i.e.
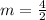 i.e.
i.e.
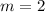 .
.
Putting this 'm' in the general form and using the point B( -1,1 ), we get the y-intercept as,
y = mx + b i.e. 1 = 2 × (-1) + b i.e. b = 3.
So, the equation of AB is y = 2x + 3.
Also, slope of BC is
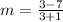 i.e.
i.e.
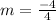 i.e.
i.e.
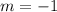 .
.
Putting this 'm' in the general form and using the point B( -1,1 ), we get the y-intercept as,
y = mx + b i.e. 1 = (-1) × (-1) + b i.e. b = 0.
So, the equation of BC is y = -x.
2. We will find the slope of line perpendicular to AB and BC.
When two lines are perpendicular, then the product of their slopes is -1.
So, slope of line perpendicular to AB is
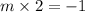 i.e.
i.e.
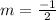
So, slope of line perpendicular to BC is
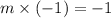 i.e. m = 1.
i.e. m = 1.
3. We will now find the equations of line perpendicular to AB and BC.
Using the slope of line perpendicular to AB i.e.
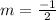 and the point opposite to AB i.e. C( 3,3 ), we get,
and the point opposite to AB i.e. C( 3,3 ), we get,
y = mx+b i.e.
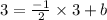 i.e.
i.e.
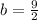
So, the equation of line perpendicular to AB is

Again, using the slope of line perpendicular to BC i.e. m = 1 and the point opposite to BC i.e. A( -3,3 ), we get,
y = mx + b i.e. 3 = 1 × -3 + b i.e. b = 6.
So, the equation of line perpendicular to BC is y = x+6
4. Finally, we will solve the obtained equations to find the value of ( x,y ).
As, we have y = x+6 and
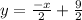
This gives,
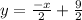 →
→
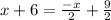 → 2x+12 = -x+9 → 3x = -3 → x = -1.
→ 2x+12 = -x+9 → 3x = -3 → x = -1.
So, y = x+6 → y = -1+6 → y=5.
Hence, the orthocenter of the ΔABC is ( -1,5 ).