Question

Write the quadratic equation whose roots are 6 and 3, and whose leading coefficient is 4

(Use the letter x to represent the variable)

Answer 1

If α and β are the Roots of a Quadratic Equation ax² + bx + c then :

✿ Sum of the Roots : α + β
`\mathsf{= (-b)/(a)}`

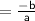
✿ Product of the Roots : αβ
`\mathsf{= (c)/(a)}`

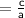
Let the Quadratic Equation we need to find be : ax² + bx + c = 0

Given : The Roots of a Quadratic Equation are 6 and 3

⇒ α = 6 and β = 3

Given : The Leading Coefficient of the Quadratic Equation is 4

Leading Coefficient is the Coefficient written beside the Variable with Highest Degree. In a Quadratic Equation, Highest Degree is 2

Leading Coefficient of our Quadratic Equation is (a)

⇒ a = 4

⇒ Sum of the Roots
`\mathsf{: (6 + 3) = (-b)/(4)}`

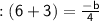
⇒ -b = 9(4)

⇒ b = -36

⇒ Product of the Roots
`\mathsf{: (6 * 3) = (c)/(4)}`

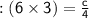
⇒ c = 18 × 4

⇒ c = 72

⇒ The Quadratic Equation is 4x² - 36x + 72 = 0