Question

What is the solution to the following system?

(2, 3, 4)

(4, 3, –2)

(4, 3, 2)

(6, 7, –2)

Answer 1

C on edge

Explanation:

: )

Answer 2

(4,3,2)

Explanation:

We can solve this via matrices, so the equations given can be written in matrix form as:

`\left[\begin{array}{cccc}3&2&1&20\\1&-4&-1&-10\\2&1&2&15\end{array}\right]`

Now I will shift rows to make my pivot point (top left) a 1 and so:

`\left[\begin{array}{cccc}1&-4&-1&-10\\2&1&2&15\\3&2&1&20\end{array}\right]`

Next I will come up with algorithms that can cancel out numbers where R1 means row 1, R2 means row 2 and R3 means row three therefore,

-2R1+R2=R2 , -3R1+R3=R3

`\left[\begin{array}{cccc}1&-4&-1&-10\\0&9&4&35\\0&14&4&50\end{array}\right]`

`(R_2)/(9)=R_2`

`\left[\begin{array}{cccc}1&-4&-1&-10\\0&1&(4)/(9)&(35)/(9)\\0&14&4&50\end{array}\right]`

4R2+R1=R1 , -14R2+R3=R3

`\left[\begin{array}{cccc}1&0&(7)/(9)&(50)/(9)\\0&1&(4)/(9)&(35)/(9)\\0&0&-(20)/(9)&-(40)/(9)\end{array}\right]`

`-(9)/(20)R_3=R_3`

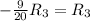
`\left[\begin{array}{cccc}1&0&(7)/(9)&(50)/(9)\\0&1&(4)/(9)&(35)/(9)\\0&0&1&2\end{array}\right]`

`-(4)/(9)R_3+R_2=R2` ,
`-(7)/(9)R_3+R_1=R_1`

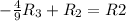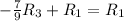
`\left[\begin{array}{cccc}1&0&0&4\\0&1&0&3\\0&0&1&2\end{array}\right]`

Therefore the solution to the system of equations are (x,y,z) = (4,3,2)

Note: If answer choices are given, plug them in and see if you get what is "equal to". Meaning plug in 4 for x, 3 for y and 2 for z in the first equation and you should get 20, second equation -10 and third 15.