Question

Find a polynomial f(×) with leading coefficient 1 such that the equation f(×)=0 has The given roots and no others . Root 1, -5 multiplicity 2,1

Answer 1

`x^(3) +3x^(2)-9x+5 = 0`

Explanation:

We are given that the only roots of the given polynomial f(x) are 1 and -5 with multiplicity (the number of times the roots are repeating) 2 and 1 respectively.

Also, it is provided that the function satisfy that f(x)=0.

So, comparing the two information we have that,

f(x) = 0 and 1, -5 are the roots of f(x),

i.e
`(x-1)^(2) * (x+5) = 0`

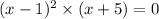
i.e.
`(x^(2) +1-2x) * (x+5) = 0`

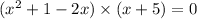
i.e.
`x^(3) +3x^(2)-9x+5 = 0`

Also, we can see that ths polynomial has leading co-efficient 1 i.e. the co-efficient of highest degree variable i.e. x^{3}.

Hence, the polynomial having leading co-efficient 1 and roots 1, -5 is
`x^(3) +3x^(2)-9x+5 = 0`.