Question

PLEASE HELP!! Algebra 2 Review !!

1. What is the equation, in standard form, of a parabola that models the values in the table?

x | -2 0 4
f(x) | 2.5 1.5 -60.5
(I used STAT on the calculator, and found the answer, nevermind on this one)

2. Simplify the expression.

`(5 + 6i)/(4 + 6i)`

Answer 1

`(28-3i)/(26)`

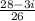
Explanation:

For #2, remember that
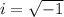`i=√(-1)`, so
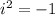`i^(2)=-1` Also, (a+b)(a-b), where a and b are any numbers, (a+b)(a-b)=
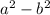`a^2-b^2`. Now, to simplify, or radicalize, a number with surds in the denominator, you have to multiply the denominator by its conjugate. If there is a complex number
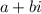`a+bi`, where a and b are any numbers, the conjugate is always
`a-bi`. Lets apply these rules. The conjugate of 4+6i is 4-6i, so do this:

`(5+6i)/(4+6i)=((5+6i)(4-6i))/((4+6i)(4-6i))=(20+24i-30i+36)/(16+36)=(56-6i)/(52)=(2(28-3i))/(2(26))=(28-3i)/(26)`

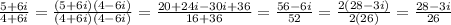
Our answer is (28-3i)/(26)!