Question

∫
`(dx)/((1+x^(2) )arccotx)` What is the equivalent of integral?

Answer ㏑
`(1)/(arctanx)+c`
Please explain ^-^

Answer 1

`\displaystyle\int(\mathrm dx)/((1+x^2)\cot^(-1)x)`

Recall that
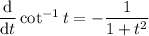`(\mathrm d)/(\mathrm dt)\cot^(-1)t=-\frac1{1+t^2}`. So suppose we substitute
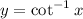`y=\cot^(-1)x`, so that
`\mathrm dy=-(\mathrm dx)/(1+x^2)`. Then the integral becomes

`\displaystyle-\int\frac{\mathrm dy}y=-\ln|y|+C`

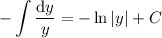
and replacing
`y` for
`x` gives the antiderivative

`-\ln|\cot^(-1)x|+C=\ln\frac1+C`

The proposed answer is not correct. Differentiating gives

`(\mathrm d)/(\mathrm dx)\ln\frac1{\tan^(-1)x}=-(\mathrm d)/(\mathrm dx)\ln\tan^(-1)x=-((\mathrm d)/(\mathrm dx)\tan^(-1)x)/(\tan^(-1)x)=-\frac1{(1+x^2)\tan^(-1)x}`

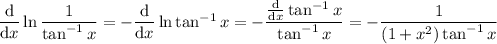
(Note the negative sign. We can also omit the absolute sign if we use a particular definition for
`\cot^(-1)x`, but I don't think it's necessary to go into too much detail.)