Question

To determine the trajectory of the movement of a material point in the xOz plane that is subjected simultaneously to oscillations x (t) = A * sin π(t + 1) and y (t) = A * sin (πt + π / 2).

Answer 1

We are to show that the given parametric curve is a circle.

The trajectory of a circle with a radius r will satisfy the following relationship:

`(x-x_c)^2 + (y-y_c)^2 = r^2`

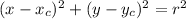
(with (x_c,y_c) being the center point)

We are given the x and y in a parametric form which can be further rewritten (using properties of sin/cos):

`x(t) = A\sin \pi(t+1) = A\sin (\pi t + \pi) = -A\sin \pi t\\y(t) = A\sin (\pi t + (\pi)/(2)) = A\cos \pi t`

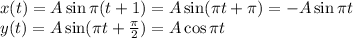
Squaring and adding both gives:

`x^2(t) + y^2(t) = A^2(-1)^2\sin^2 \pi t + A^2 \cos^2 \pi t = A^2\\\implies x^2 + y^2 = A^2`

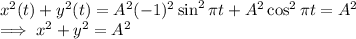
The last expression shows that the given parametric curve is a circle with the center (0,0) and radius A.