Answer: (B) 3 times as fast
Explanation:
rate of change is the "slope" between the given interval.
f(x) = 125(.9)ˣ
f(1) = 125(.9)¹
= 112.5
f(5) = 125(.9)⁵
= 73.8
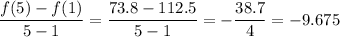
********************
f(11) = 125(.9)¹¹
= 39.2
f(15) = 125(.9)¹⁵
= 25.7
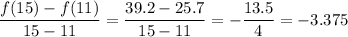
********************
The rate of change from years 1 to 5 is approximately 3 times the rate of change from years 11 to 15.