Answer:
Anya rode at 8.5 miles per hour.
Explanation:
We have been given that Taylor and Anya live 63 miles apart. One day they left their houses at 8 am and met at 11 am riding toward each other. Taylor rode at 12.5 miles per hour.
We can see that Taylor and Anya met after 3 hours as 11-8=3. This means that both rode their cycles for 3 hours.
Let us find distance covered by Taylor.
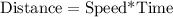
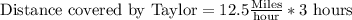
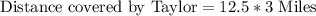

Therefore, Taylor covered 37.5 miles in 3 hours.
Let us find distance covered by Anya in 3 hours by subtracting distance covered by Taylor from total distance of 63 miles.
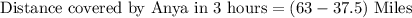
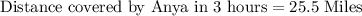
Now let us find speed at which Anya rode bike.
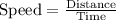

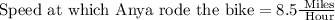
Therefore, Anya rode the bike at the speed of 8.5 miles per hour.