Question

Is the following expression true or false? [x^2 + 8x + 16] · [x^2 – 8x + 16] = (x2 – 16)^2

Answer 1

`(x^(2) +8x+16)(x^(2) -8x+16)\\(x+4)^(2) (x-4)^(2) \\(x^(2)-16)^(2) \\`

it is true; just work them out, you should get what they got :))

Answer 2

True.

Explanation:

We have been given an equation
`[x^2 + 8x + 16]\cdot [x^2- 8x+16] = (x^2-16)^2`. We are asked to determine whether our given equation is true or false.

To answer our given problem, we will simplify left side of our given equation using distributive property as:

`x^2(x^2- 8x+16)+ 8x(x^2- 8x+16)+16(x^2- 8x+16)`

`x^4- 8x^3+16x^2+ 8x^3-64x^2+128x+16x^2-128x+256`

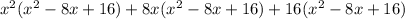
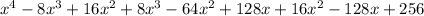
Combine like terms:

`x^4- 8x^3+ 8x^3+16x^2+16x^2-64x^2+128x-128x+256`

`x^4-32x^2+1256`

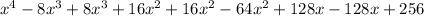
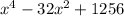
Now, we will expand right side of our given equation using perfect square formula as:

`(x^2-16)^2=(x^2)^2-2(x)(16)+16^2`

`(x^2-16)^2=x^4-32x+256`

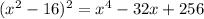
Since both sides of our given equation are equal, therefore, our given statement is true.