Answer:
The solution set is { x | x
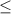 -2 or x
-2 or x
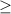 1}
1}
Explanation:
The given inequality is
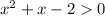
Let us factor
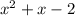
so we have
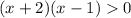
Let us find zeros of
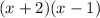
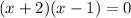
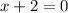 or
or
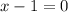
 or
or

so we have intervals (-∞ , -2) , (-2 , 1) and (1, ∞)
we need to find in which interval is
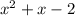 is greater than 0
is greater than 0
so we will assume the value of x in each interval and will plug it in
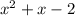 and will check if we get negative or positive value
and will check if we get negative or positive value
Let us check the sign of
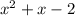 in (-∞ , -2)
in (-∞ , -2)
we can take x=-3 and plug it in
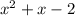
so we have
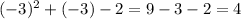 ( which is greater than 0)
( which is greater than 0)
This shows (-∞, -2) is one of the solution set
similarly we can check the sign of
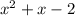 in (-2,1)
in (-2,1)
we take x= 0 , so we have
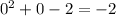 ( which is less than 0)
( which is less than 0)
This shows (-2,1) is not the solution set
now we check the sign of
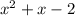 in (1 ,∞)
in (1 ,∞)
we can assume x= 2, so we have
 ( which is greater than 0)
( which is greater than 0)
This shows (1 ,∞) is the solution set
Hence the solution set in interval notation (∞ ,-2)∪(1,∞)
we can write this as { x | x
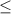 -2 or x
-2 or x
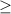 1}
1}