Question

Which equation could generate the curve in the graph below?

y = 9x2 + 6x + 4
y = 6x2 – 12x – 6
y = 3x2 + 7x + 5
y = 2x2 + 8x + 8

Answer 1

It's D. on EtDtGtE

Explanation:

Answer 2

y = 2x^2 + 8x + 8

Explanation:

The graph touches the x axis at only one point.

so there is only one real solution.

If there is only one real solution then determinant =0

Now we find out the equation that has determinant 0

Determinant is
`b^2 - 4ac`

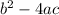
Let find b^2 - 4ac for each equation

(a)
`y = 9x^2 + 6x + 4`

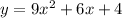
a= 9 , b = 6 and c=4

`b^2-4ac= 6^2 - 4(9)(4) = -108`

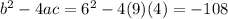
determinant not equal to 0

(b)
`y = 6x^2 – 12x – 6`

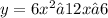
a= 6 , b = -12 and c=-6

`b^2-4ac= (-12)^2 - 4(6)(-6) = 288`

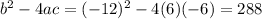
determinant not equal to 0

(c)
`y = 3x^2 + 7x + 5`

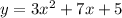
a= 3 , b = 7 and c=5

`b^2-4ac= (7)^2 - 4(3)(5) = -11`

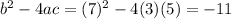
determinant not equal to 0

(d)
`y = 2x^2 + 8x + 8`

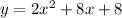
a= 2 , b = 8 and c=8

`b^2-4ac= (8)^2 - 4(2)(8) = 0`

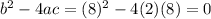
determinant equal to 0. So there is only one real solution.