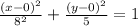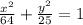Question

Write the equation of the conic section with the given properties:

An ellipse with vertices (-8, 0) and (8, 0) and a minor axis of length 10.

Answer 1

`(x^2)/(64) + (y^2)/(25) =1`

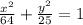
Explanation:

An ellipse with vertices (-8, 0) and (8, 0)

Distance between two vertices = 2a

Distance between (-8,0) and (8,0) = 16

2a= 16

so a= 8

Vertex is (h+a,k)

we know a=8, so vertex is (h+8,k)

Now compare (h+8,k) with vertex (8,0) and find out h and k

h+8 =8, h=0

k =0

a minor axis of length 10.

Length of minor axis = 2b

2b = 10

so b = 5

General formula for the equation of horizontal ellipse is

`((x-h)^2)/(a^2) + ((y-k)^2)/(b) =1`

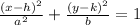
a= 8 , b=5 , h=0,k=0. equation becomes

`((x-0)^2)/(8^2) + ((y-0)^2)/(5) =1`

`(x^2)/(64) + (y^2)/(25) =1`