Question

Find the area of a rectangle whose vertices are (2,2),(-3,2),(2,8), and (-3,8)

Answer 1

Area of rectangle = 30 units

Explanation:

vertices are (2,2),(-3,2),(2,8), and (-3,8)

Let find the distance between (2,2) and (2,8). because they have same x values. that would be our width

distance =
`√((x_2-x_1)^2 + (y_2-y_2)^2)`

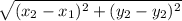
D =
`√((2-2)^2 + (8-2)^2)=\sqrt(6^2) = 6`

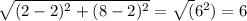
Width = 6

Now we find distance between (2,2) and (-3,2) because they have same y values, that would be our length

distance =
`√((x_2-x_1)^2 + (y_2-y_2)^2)`

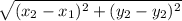
D =
`√((-3-2)^2 + (2-2)^2)=\sqrt(-5^2) = \sqrt(25)= 5`

length = 5

Area of rectangle = length * width = 5*6 = 30