Question

The company also discovered that it costs $25 to produce 2 camera cases, $59 to produce 4 camera cases and $305 to produce 10 camera cases . Find the total cost of producing 5 camera cases

Please help!!!

Answer 1

Cost of 5 camera cases is $85.

Explanation:

First we need to determine what type of function we're dealing with, is it linear, quadratic or exponential? We can determine this by calculating the first difference.

We can translate the number of cameras to correspond to the x axis and cost to the y axis. By doing this we can come up with the ordered pairs of (2,25), (4,59),(10,305). Let's get the first two ordered pairs and calculate the first difference:

`(59-25)/(4-2)=17`

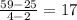
And now the second and third value:

`(305-59)/(10-4)=41`

Notice how these values do not match, this means that this function is not increasing at a constant rate meaning that this function is not linear. Now let's calculate the second difference:

`(41-17)/(10-2)=3`

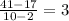
This means our function is quadratic with a=3. Remember that generally speaking a quadratic function is such that:

`y=ax^2+bx+c`

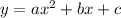
Where a,b,c are coefficients and in this case a=3. Now, let's solve for b and c values by using the coordinates given. Let's use the coordinates (2,25) where x=2 and y=25 and so:

`f(x)=ax^2+bx+c\\\\25=3(2)^2+b(2)+c\\25=3(4)+2b+c\\25=12+2b+c\\13=2b+c\\\\b=(13-c)/(2)`

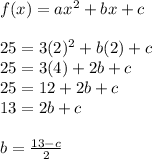
Now let's solve for "c" by using different coordinates (4,59) where x=4 and y=59 and also use the "b" value that we calculated above and so:

`f(x)=ax^2+bx+c\\\\59=3(4)^2+((13-c)/(2))(4)+c\\59=48+(52-4c)/(2)+c\\11=(52-4c+2c)/(2)\\11=26-2c+c\\-15=-c\\\\c=15`

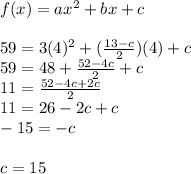
Now that we know the value of "c" we can use the equation for b to solve for b and so:

`b=(13-c)/(2)=(13-15)/(2)\\\\b=-1`

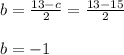
So this means in the quadratic equation a=3, b=-1 and c=15 therefore by using the general equation of a quadratic function we obtain or final equation:

`f(x)=ax^2+bx+c\\\\f(x)=3x^2-x+15`

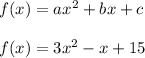
Since we want to find the total cost of producing 5 camera cases x=5 and so:

`f(x)=3x^2-x+15\\\\f(5)=3(5)^2-(5)+15\\f(5)=75-5+15\\\\f(5)=85`

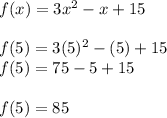
And so the cost of 5 camera cases is $85.