Question

What is the value of arccos (-1/2)

Answer 1

120° & 240° (given the angles are between 0° and 360°)

Explanation:

We want to find
`arccos(-(1)/(2))`.

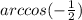This means we want to know the angle(s) for which cosine has a value of
`-(1)/(2)`.

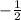The basic acute angle that has a cosine of
`(1)/(2)` is 60°. But we want to know NEGATIVE
`(1)/(2)`. So in which quadrants is cosine negative? Second and Third

• The rule to find 2nd quadrant angle with known acute angle is: 180 - α
• The rule to find 3rd quadrant angle with known acute angle is: 180 + α

Where α is the basic acute angle (in our case it is 60°)

So 2nd quadrant angle is 180 - 60 = 120°

and 3rd quadrant angle is 180 + 60 = 240°

Answer 2

120°

Explanation:

arccos means the inverse of cosine.

arccos (-1/2) ⇒ We can rewrite this equation as;

cosФ = 1/2 Find the value of Ф.

Ф = arccos (-1/2) ⇒ This can be calculated directly from the calculator.

arccos (-1/2) = 120°

or arccos (-1/2) = (180 + 60)

= 240°

You can have more than one value of arccos (-1/2) since the cosine is negative in the second and third quadrant.