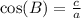Answer:
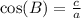
Explanation:
We have been given a triangle. We are asked to find
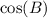 .
.
We know that cosine relates adjacent side of a right triangle to its hypotenuse.
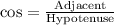
We can see that side AB is adjacent side and CB is hypotenuse of our given right triangle.
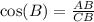
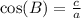
Therefore, our required value is