Answer:
The equation of the parabola in vertex form is
 .
.
Explanation:
Since the directrix is of the
 , then the equation of the parabola in vertex form is of the form:
, then the equation of the parabola in vertex form is of the form:
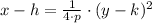 (1)
(1)
Where:
 - Dependent variable.
- Dependent variable.
 - Independent variable.
- Independent variable.
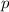 - Least distance between focus and directrix.
- Least distance between focus and directrix.
 ,
,
 - Coordinate of the vertex.
- Coordinate of the vertex.
The least distance between focus and directrix is determined by Pythagorean Theorem:

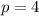
Now, we determine the location of the vertex by the following vectorial formula:
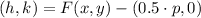 (2)
(2)
If we know that
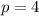 and
and
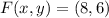 , then the location of the vertex is:
, then the location of the vertex is:

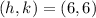
And the equation of the parabola in vertex form is
 .
.