Answer:
1.
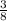
2.
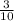
Step-by-step explanation:
The problems above tackle on the "multiplication of fractions."
Let's solve.
a.
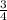 x
x
 =
=
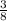
- All you have to do is to multiply the numerator of one fraction to the other, and also multiply the denominator of one fraction to the other.
- Numerator: 3x1 = 3
- Denominator: 4x2 = 8
b.
 x
x
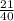 ⇒
⇒
 x
x
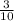 =
=
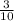
- All you have to do is to get the "Greatest Common Factor" among the fractions. The GCF of 4 and 40 is 4, so you have to divide both of them by 4. The GCF of 7 and 21 is 7, so you have to divide both of them by 7.