Question

Solve x2 + 12x + 6 = 0 using the completing-the-square method.

A) x = negative six plus or minus the square root of thirty

B) x = six plus or minus the square root of thirty

C) x = negative six plus or minus the square root of six

D) x = six plus or minus the square root of six

Answer 1

The correct answer is A

`x=-6\pm √(30)`

Step-by-step explanation:

The given expression is

`x^2+12x+6=0`

Add
`-6` to both sides

`x^2+12x=-6`

Add
`((12)/(2) )^2=(6)^2` to both sides.

`x^2+12x+(6)^2=-6+(6)^2`

We got a perfect square on the left hand side

`(x+6)^2=-6+36`

Simplify the left hand side to get,

`(x+6)^2=30`

Take square root of both sides

`(x+6)=\pm √(30)`

Solve for
`x`.

`x=-6\pm √(30)`

Answer 2

Option A is correct.

`x = -6 \pm √(30)`

Step-by-step explanation:

Given the expression:
`x^2+12x+6 = 0`

`x^2+12x+6=0`

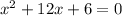
Subtract 6 from both sides, we get

`x^2+12x=-6`

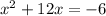
halve linear coefficient,then square it, and add it to both sides

`x^2+12x+36=30`

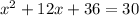
Now, the left side is a perfect square

`(x+6)^2=30`

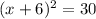
Now, take square root to both sides.

`x+6=√(30)`

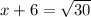
Subtract 6 from both sides, we get;

`x = -6 \pm √(30)`

So, the solutions are :
`x = -6 \pm √(30)`