Answer:
Point (1,8)
Explanation:
We will use segment formula to find the coordinates of point that will partition our line segment PQ in a ratio 3:1.
When a point divides any segment internally in the ratio m:n, the formula is:
![[x=(mx_2+nx_1)/(m+n),y= (my_2+ny_1)/(m+n)]](https://img.qammunity.org/2019/formulas/mathematics/college/rmrep3cjlzov8nvl3mqsp9wsyk8mdazuwj.png)
Let us substitute coordinates of point P and Q as:
 ,
,
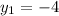
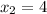
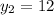
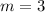
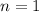
![[x=((3*4)+(1*-8))/(3+1),y=((3*12)+(1*-4))/(3+1)]](https://img.qammunity.org/2019/formulas/mathematics/college/4c4bi0sq2mms8l9vl4bfrvsvct7nk8qi3j.png)
![[x=(12-8)/(4),y=(36-4)/(4)]](https://img.qammunity.org/2019/formulas/mathematics/college/sjrh3t4qhbt3jzjqwf1u56gx28f43fhzi2.png)
![[x=(4)/(4),y=(32)/(4)]](https://img.qammunity.org/2019/formulas/mathematics/college/5htqp9x6zalzzxyz5g62dsdxkut42ekyfh.png)
![[x=1,y=8]](https://img.qammunity.org/2019/formulas/mathematics/college/xmduekvxl2kbba8pjm0rowdonbtpm6kph1.png)
Therefore, point (1,8) will partition the directed line segment PQ in a ratio 3:1.