Answer:
The answer is below
Explanation:
a) The integral
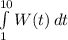 means the total change in level of water in inches from 1 am to 10 am. That is the water level change measured in inches between 1 am and 10 am
means the total change in level of water in inches from 1 am to 10 am. That is the water level change measured in inches between 1 am and 10 am
b) 7 pm is represented as t = 19 hours, while midnight is represented as t = 24 hours, hence the water level change between 7 pm and midnight is:
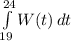
c) Using casio calculator to evaluate the integral gives:
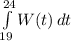 = 2.54 inches
= 2.54 inches
D) The total daily change in water level =
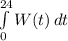 = 0.35 inches
= 0.35 inches