Question

Select the correct answer.

Taylor wants to purchase a car with an auto loan. He can get a 48-month loan from his bank that is compounded monthly at an annual Interest

rate of 7.996.

Suppose Taylor needs to obtain a loan for $19,076 to purchase the car.

Use the formula for the sum of a finite geometric series to determine Taylor's approximate monthly payment.

Fple)

P =

1- (1 + i)-

OA. Taylor's approximate monthly payment for the loan will be $458.35.

ОВ. Taylor's approximate monthly payment for the loan will be $413.22.

OC. Taylor's approximate monthly payment for the loan will be $546.90.

OD. Taylor's approximate monthly payment for the loan will be $464.81.

Answer 1

The exact monthly payment will be $465.66

From the given options: OD is the most closer

Explanation:

We got the following situation:

`\sum\limits^n_0 {C/(1+i)^n} = C+ C/(1+i)+C/(1+i)^2 + ... + C/(1+i)^n\\\\\sum\limits^n_0 {C/(1+i)^n} = C / ( 1 + 1/(1+i) + 1/(1+i)^2 + ... + 1/(1+i)^n)\\\\C \sum\limits^n_0 {(1+i)^(-n)} = C (1-(1+i)^(-n))/(1 - (1+i))`

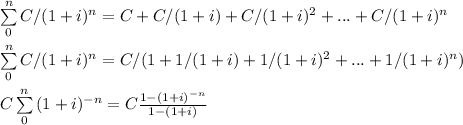
We end up with the formula for the present value of an annuity.

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

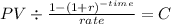
PV $ 19,076.00

time 48

rate (0.07966 / 12 months) 0.006663333

`19076 / (1-(1+0.006663)^(-48) )/(0.006663) = C\\`

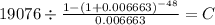
C $ 465.66509