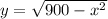Question

What is the equation of the height of a roller coaster that is 30 feet above the ground, is in a shape of a half circle and the general form of a circle with the center at the origin is x2 +y2 = r2?

Answer 1

x^2+y^2=900Explanation:

1.Write the equation that models the height of the roller coaster.

x^2+y^2=30^2

2.Start by writing the equation of the circle. (Recall that the general form of a circle with the center at the origin is x2 + y2 = r2. (10 points)

x^2+y^2=900

3.Now solve this equation for y. Remember the roller coaster is above ground, so you are only interested in the positive root. (10 points)

y= √(900-x^2)

Answer 2

Answer:
`\bold{y = √(900-x^2)}`

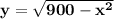
Explanation:

The general form of a circle is: (x - h)² + (y - k)² = r² ; where

• (h, k) is the center
• r is the radius

Since the roller coaster is centered at the origin, then (h, k) = (0, 0)

Since the height of the roller coaster is 30, then radius (r) = 0

Equation of the circle is: (x - 0)² + (y - k)² = 30²

⇒ x² + y² = 900

To find the equation of the semicircle, solve for "y"

x² + y² = 900

y² = 900 - x²

`√(y^2)=√(900-x^2)`

`y = \pm√(900-x^2)`

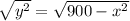
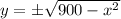
Since we are looking for the top half of the semicircle (because it is above ground), then use the positive root:
`y = √(900-x^2)`